Rückgekoppelte Schieberegister
Anders als bei den klassischen Blockchiffren wie DES oder Rijndael, bei denen
immer jeweils ein Block in mehreren Durchläufen verwürfelt wird, handelt es
sich hierbei um ein Stromchiffre. Das zentrale Element ist ein Zufallsgenerator, der
ein reproduzierbares "Rauschen" erzeugt, welches dem Klartext byteweise aufaddiert wird.
Dieser Byte-Strom, hat gute statistische Eigenschaften
(im Schnitt genau so viele Nullen wie Einsen). Die zugrundeliegende mathematische
Polynomdivision wird technisch mit mehrfach rückgekoppelten Schieberegistern
realisiert.
Ein einzelnes Schieberegister reicht aber nicht aus, weil dessen Generatorpolynom ganz
schnell bestimmt werden kann, hat man nur ein paar Bits der Folge verläßlich
erkannt.
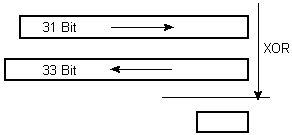
Deshalb bilden zwei gegensinnig umlaufende Register (31 bit und 33 bit) die Summanden
für eine Modulo-2-Addition (XOR). Ein drittes Register (64 bit) entscheidet, ob der
Funktionswert gültig ist oder verworfen wird.
31-bit-Register
Dieses Register hat eine Umlauflänge von 2^31-1 = 2147483647. Das ist eine Primzahl
die garantiert, daß alle Folgemaßnahmen diese Länge vervielfachen
und sich nicht durch zufällig erwischte Teiler kurze Zyklen wiederholen.
Der Schlüssel wählt ein Rückkopplungspolynom aus einer Liste primitiver
Polynome aus. Diese Polynome sind alle irreduzibel. Jeder Wert des Registers liegt damit
auf dem großen Zyklus.
33-bit-Register
Das Rückkopplungspolynom für dieses Register wird direkt vom Schlüssel
abgeleitet. Das heißt, daß sich hier nur zufällig ein Maximalzyklus
ergibt. Die Umlaufsequenzen können sehr viel kürzer sein aber das weiß
man nicht.
Der Vorteil besteht darin, daß das Polynom, welches die Sequenz bestimmt,
unbekannt ist und auch nicht vorhergesagt werden kann. 2147483648 verschiedene Polynome
sind in der aktuellen Implementierung möglich.
64-bit-Register und Butt
Dieses Register wird genau wie das 33-bit-Register mit einem zufälligen Polynom
betrieben, welches direkt vom Schlüssel abgeleitet wird. Aus Performance-Gründen
ist die Anzahl der möglichen Polynome ebenfalls auf 2147483648 beschränkt.
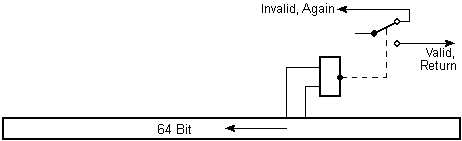
Während das Register umläuft, greift ein "Kolben" ins Getriebe und fühlt
den Inhalt von zwei zufällig ausgewählten Bits ab. Nur wenn diese beiden Bits
Null sind, wird die oben berechnete Verknüpfung von 31-bit- und 33-bit-Register als
Funktionswert ausgegeben. Im Durchschnitt werden also 3/4 aller Werte verworfen (manchmal
nur die Hälfte, aber wann, das weiß man wieder nicht). Der Butt kann so nochmal
528 unterschiedliche Untersequenzen auswählen.
Schlüsselgenerierung mit MD5
Aus der eingegebenen Passphrase berechnet der MD5-Algorithmus eine 128-bit-Zahl, also
16 byte. Diese initialisieren die Startwerte für die umlaufenden Schieberegister.
Anschließend wird der Key noch einmal durch den MD5-Algorithmus geschickt und die
Rückkopplungspolynome davon abgeleitet.
ASCII-Kompression und Base64-Kodierung
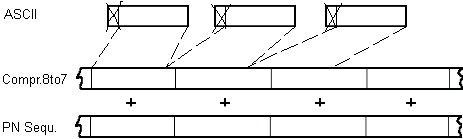
Der Klartext ist reiner ASCII-Text. Um nicht jedes achte Bit der Schlüsselsequenz
zu verraten, werden die ASCII-Bytes vor der Verschlüsselung auf 7 bit
zusammengeschoben und nach der Entschlüsselung wieder expandiert.
Der verschlüsselte Bytestrom muß noch in sein Trägermedium integriert
werden, nämlich in eine html-Seite. Das geht aber so roh nicht, weil alle Zeichen
im Wertevorrat von 128 bis 255 nicht zum ASCII-Code gehören und selbst im unteren
Bereich Sonderzeichen umkodiert oder Dos2Unix oder sonstwas gewandelt werden
könnten. Deshalb wird der Bytestrom nochmal 6-bit-weise zerstückelt und mit
den in allen ASCII-Codes der Welt einheitlichen Buchstaben und Ziffern kodiert (Base64).
Dieser Block in einer html-Seite sollte von keiner Code-Umrechnung verunstaltet
werden.
|