Feedback Shift Registers
Unlike the classic block codes e.g. DES or Rijndael which always scramble a block
in several loops, here we have a stream cipher. The central element is a
randomizer that generates a reproducible "noise" which is added to the plaintext
byte by byte. This byte current has good statistical qualities. On average there
are as many ones as zeros. The underlying mathematical polynomial division is
implemented technically with multiple coupled feedback shift registers.
However, a single shift register is not sufficient, because its characteristic
polynomial can be determined quite fast when only a couple of bits of the
sequence have been recognized.
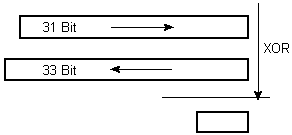
Therefore two reversely circulating registers (31 bits and 33 bits) were selected
as operands for a bitwise addition modulo 2 (XOR). A third register (64 bits)
decides whether the value of the function is valid or gets rejected.
31-bit Register
This register has a sequence length of 2^31-1 = 2147483647. That is a prime
number which guarantees that the following methods multiply this length and that
short cycles caused by randomly caught factors won't occur.
The key selects a feedback polynomial from a list of primitive polynomials. All
these polynomials are irreducible. Every register value is then part of a maximum
ring yield.
33-bit Register
The feedback polynomial for this register is derived from the key directly. This
means that a maximum cycle arises here only by chance. The circulation sequences
can be very much shorter but it is unknown when.
The advantage consists in the fact that the polynomial which determines the
sequence is unknown and cannot be predicted either. 2147483648 different
polynomials are possible in the current implementation.
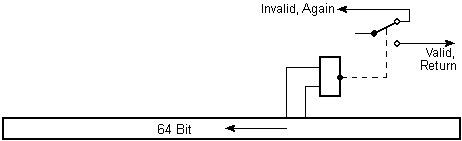
64-bit Register and Butt
This register operates exactly like the 33-bit register with a coincidental
polynomial which is derived of the key directly. For performance reasons the
number of the possible polynomials is confined also to 2147483648.
While the register circulates, a "butt" intrudes on the transmissions and detects
the contents of two randomly selected bits. Only if these two bits are zero, the
combination of 31 bit and 33 bit which was calculated above, is issued as return
value of the function. Well, in the average 3/4 of all results are thrown away
(sometimes only half of the results, but when this occurs is unknown again). The
butt can select 528 various sub-sequences respectively.
Key Generation with MD5
From the entered passphrase the MD5 algorithm calculates a 128-bit number, which
are 16 bytes. Those initialize the start values for the circulating shift
registers. After that the key is sent through the MD5 algorithm again to derive
the feedback polynomials.
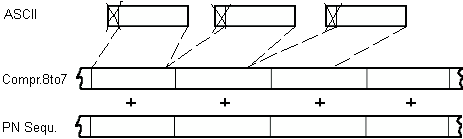
ASCII Compression and Base64 Coding
The plaintext is pure a ASCII text. In order not to betray every eighth bit of
the key sequence, the ASCII bytes are compressed to 7 bits before encoding and
expanded after the deciphering again.
The encoded byte stream still needs to be integrated in its carrier, namely into
a html page. However, this won't work in the somewhat raw state, because none of
the characters in the set
of values between 128 and 255 are part of the ASCII code, and even in the
standard ASCII section special signs could be re-coded, Dos2Unix changed or
something else. Therefore the byte stream is cut into 6 bit pieces which are
encoded with standard ASCII characters (Base64). It shouldn't be possible to
disfigure the now resulting block on a html page by any code conversion.
|