Zirka 3 Milliarden Jahre mussten wir darauf warten, dass sich unsere Vorfahren, die Bakterien, irgendwie sinnvoll zusammen rotteten, um mehrzellige Wesen zu bilden. Mag man das jetzt Zufall oder Statistik nennen, die nächsten Zufälle gingen jedenfalls etwas schneller.

Vor 360 Millionen Jahren lebte Acanthostega gunnari in flachen Gewässern der urzeitlichen Erde. Er war einer der ersten Tetrapoden, Tiere, die schon vier Beine hatten und sich später zu den erfolgreichen Reptilien entwickeln sollten.

Acanthostega war noch nicht so weit. Er schwamm noch ausschließlich im Wasser, konnte aber schon mit seinen Gliedmaßen im Schlamm rumwühlen, Wurzeln beiseite schieben, sich festklammern und was sonst noch ein junges Amphibienherz begehrt.

Articulated skeleton. Geological Museum, Copenhagen MGUH Field number 1227. Photo M. Coates. Copyright © 1997 University Museum of Zoology, Cambridge.

Sensationell bei diesem Fossilienfund aus Grönland war die Tatsache, dass Acanthostega offensichtlich acht Finger hatte. Acht Finger! Das macht an beiden Vorderfüßen zusammen sechszehn. Genial!

Aber dann hat die Evolution einen entscheidenden Fehler gemacht. Denn die ersten Reptilien, die an Land gekrochen kamen, hatten nur noch fünf Finger. Herr Gott - warum hast Du damals nicht Acanthostega gunnari raus an's Ufer geschickt?

350 Millionen Jahre lang hat das niemanden gestört. Im Gegenteil, wir fanden es sogar noch lustig, einen der fünf Finger vorteilhaft zum Daumen umzufunktionieren. Es ist nur so, dass unsere Ahnen irgenwann den Unterschied zwischen eins und viele etwas genauer wissen wollten und deshalb mit der Digitalisierung begannen. (Muss ich das jetzt erklären? lat. digitus - der Finger, digital - mit den Fingern.) In Ermangelung weiterer Finger war dann eben bei zehn Schluss. Schade.

Sechszehn - man stelle sich das mal vor. Das ist zwei hoch zwei hoch zwei. Was Besseres gibt's doch gar nicht als Zahlenbasis. Okay, wir bräuchten dann noch ein paar Zeichen für die Ziffern von zehn bis fünfzehn. Ich meine, zweckmäßigerweise hätten sich dazu die Inder mit den Arabern vor 1000 Jahren auf Figuren einigen können, die wir heute auf dem Drucker haben. Da das leider nicht der Fall ist, behelfen wir uns einfach mit den Buchstaben A..F und behaupten, das seien Ziffern der Werte zehn bis fünfzehn und nennen alles zusammen schlicht Hexadezimalsystem. Wir wissen heute, dass die geringfügig höhere Komplexität von Hex-Zahlen ohne Probleme im täglichen Leben gemeistert werden könnte, hätten wir in der Schule das kleine Einmaleins bis 8 x 8 und dann das große Einmaleins bis 16 x 16 gelernt. Es wäre im Gegenteil einfacher und so mancher Kummer wäre uns erspart geblieben.

Aber Acanthostega hat's vergeigt. Ist einfach ausgestorben und hat den Fünffinglern das Terrain überlassen.

Und so müssen wir uns heute mit dem schwierigeren Dezimalsystem rumquälen und wundern uns, warum auf dem Computer Zahlen krumm aussehen, die eigentlich gerade sind und umgekehrt.

----
Was sind eigentlich "runde Zahlen"? Was ist ein "runder" Geburtstag?
Zum Beispiel der 32. Geburtstag. Denn ab diesem kann man die Jahre nicht mehr an einer Hand abzählen. - Denkpause - Also gut, wem die digitale Zählerei zu albern ist, der könnte seinen 10000. Geburtstag feiern. Zwei Beispiele für wirklich einmalige Daten im Leben, an denen die meisten von uns völlig achtlos vorüber gehen.
----

Aber bleiben wir nochmal beim Dezimalsystem. Da können wir ja noch von Glück reden, dass es sich weltweit einheitlich durchgesetzt hat. Man stelle sich vor, die Ägypter hätten an ihrem Sexagesimalsystem (Basis 60) der Pharaonenzeit festgehalten, dessen Nachwirkungen wir heute noch bei der Uhrzeit und bei Winkelangaben spüren. Zu dumm, dass die großen Geister der Antike den Kreis in 360 Grad geteilt haben und nicht durch stetiges Halbieren in 256 Grad.

Gleiche Zahlen sind nicht gleich

Mit der aufkommenden Rechentechnik in den 50iger Jahren und zunehmenden Speichergrößen entstand schnell die Praxis, auch für Zahlen basierend auf Zweierpotenzen die gleichen Zahlenpräfixe zu verwenden wie im Dezimalsystem. Nun ist aber das Dezimalsystem so fürchterlich unrund, dass eigentlich nichts passt. Mit etwas Mut kann man eine Ähnlichkeit zwischen 2¹⁰ und 10³ erkennen. Da aber 1024 nicht 1000 ist, hat man das K (sprich "Ka") erfunden, um den Unterschied zum kilo zu dokumentieren. Damit war aber schon Schluss mit der Exaktheit, denn das große M für 1024 K war nicht mehr vom großen M für Mega zu unterscheiden. Die Differenz zwischen beiden wuchs nun schon auf 48576 an. Fortan sollte man einfach wissen, wovon die Rede war. 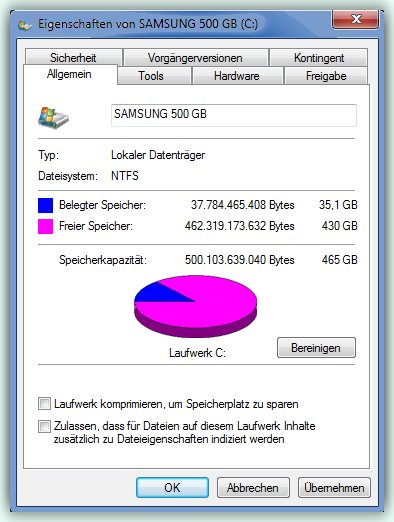Und Betriebswirtschaftler rechnen da naturgemäß anders. Meine 500 GB Platte hat 465 Gigabyte (Laufwerk C:, rechte Maustaste, Eigenschaften).

Housends and Hillions

Was wir brauchen sind unverwechselbare neue Begriffe für wichtige Größenordnungen in der binären Welt.

Hundert (engl. hundred)

• Hundert hex, entlehnt von dezimal Hundert
• Präfix: hexo
• 2⁸,  256_(dez),  100_(hex)

Hausend (engl. housend)

• entlehnt von Tausend, aber mit H am Anfang (von Hex)
• Präfix: hilo
• 2¹⁶,  65 536_(dez),  1 0000_(hex)

Hillion (engl. hillion)

• entlehnt von Million, aber mit H am Anfang
• Präfix: hega
• 2³²,  4 294 967 296_(dez),  1 0000 0000_(hex)

Hilliarde (engl. hilliard)

• entlehnt von Milliarde, aber mit H am Anfang
• Präfix: higa
• 2⁶⁴,  18 446 744 073 709 551 616_(dez),  1 0000 0000 0000 0000_(hex)

Hipion (engl. hipion)

• Kunstwort (sprich Haipjen)
• Präfix: hipa
• 2¹²⁸,  1 0000 0000 0000 0000 0000 0000 0000 0000_(hex)

Das dürfte erstmal reichen.

Ein Beispiel:
0x3a7b150c0f41 - das sind
drei a sieben be hillion eins fünf null ce hausend null eff vier eins

Oder meine Platte hat 74,7 hegabyte.

In obiger Aufstellung fehlt der Begriff für 2⁴ = 10_(hex). Die natürliche Sprache hat aber dafür keinen Präfix sondern einen Suffix. Im Dezimalsystem ist es das -zig, nun bräuchten wir ein -hig und im Englischen ein -hy.

Die Lage ist aussichtslos. Wer ist schuld?

Es war vor langer, langer Zeit ...