Big Endian bezeichnet die Schreibweise von Daten, beginnend mit dem größtwertigsten Teil zuerst. Zum Beispiel schreiben wir die Uhrzeit als Stunden, Minuten, Sekunden. Im Gegensatz dazu ist das Tagesdatum Little Endian, nämlich Tag, Monat, Jahr. Schon hier wird offensichtlich, dass diese Uneinheitlichkeit zu Problemen führt, nämlich dann, wenn z.B. mehrere Zeitangaben der Reihenfolge nach sortiert werden sollen. Beim Tagesdatum muss man von rechts beginnen, bei der Uhrzeit von links.

Jede Zahl, bestehend aus Dezimalziffern, schreiben wir im Big-Endian-Format von der größten zur kleinsten. Aber warum? Zumindest im Umgang mit positiven ganzen Zahlen, was bei weitem am häufigsten der Fall ist, wäre gerade die umgekehrte Darstellung, vom Kleinsten zum Größten, sinnvoller.

Man lese bitte (laut) die folgende Aussage, für deren Richtigkeit ich mich nicht verbürge. Soll nur das Prinzip verdeutlichen:

Deutschland hat auf einer Fläche von 35702119 Hektar
80219695 Einwohner.

Na, was gemerkt? Um überhaupt die ersten Ziffern als "35 Millionen" betiteln zu können, muss man zunächst zum Ende der Zahl, dann rückwärts Dreiergruppen bilden, und erst dann weiß man, was man sagen soll.

Würden wir hingegen mit der kleinsten Ziffer beginnen, dann könnten wir auch die Zahlen viel einfacher untereinander schreiben oder addieren, ohne am Anfang schon wissen zu müssen, wie groß denn die größte Zahl werden wird.
Zum Beispiel

Schuster  : 71 (siebzehn)
Meier     : 1402 (einundvierzigundzweitausend)
Lehmann   : 39 (dreiundneunzig)
Schmidt   : 007 (siebenhundert)
-------------------------------------------------
Summe     : 1582 (einundfünfzigachthundertzweitausend)

Es scheint so, als ob irgend jemand im frühen Mittelalter da was falsch verbunden hätte. In Europa war das Römische Zahlensystem gängiger Standard, bis eine kluge Idee aus Arabien aufgegriffen wurde. Es hat Jahrhunderte gedauert, bis sich das dezimale Stellenwertsystem mit der Null, ursprünglich aus Indien, durchgesetzt hat.

Was aber nie in Frage stand, war die Anordnungsreihenfolge der Dezimalstellen. Denn sowohl die Römer wie auch die Araber schreiben die Ziffern ihrer Zahlen mit der größtwertigsten links und der geringstwertigsten rechts. Es gibt aber einen entscheidenden Unterschied - Araber schreiben von rechts nach links!

In Europa hätte man beim Rechnen mit den modernen arabischen Ziffern diese also in ihrer Anordnungsreihenfolge umdrehen müssen. Vermutlich hat es den Versuch sogar gegeben, denn im Deutschen spricht man heute wie im Arabischen bei Zahlen bis Hundert die Einerstelle zuerst.

Im Laufe der Zeit hat sich das dezimale Stellenwertsystem mit arabischen Ziffern auf der ganzen Welt durchgesetzt, und niemand schien sich an der Big-Endian-Reihenfolge der Ziffern zu stören. Bis in den siebziger Jahren die Mikroprozessoren aufkamen und das Informationszeitalter eröffneten.

Die Firma Intel hat damals klug und weise folgende Festlegung getroffen:

"Niederwertige Daten stehen immer auf niederwertigen
Adressen und werden zeitlich zuerst abgearbeitet."

Kurz, die Vorstellungskraft der Leute beim Lesen von Programm-Listings oder bei der Entwicklung jeglicher Algorithmen wäre schlicht überfordert. Deshalb ging Intel den Kompromiss ein, Registerinhalte und Speicheradressen in gewohnter Darstellung zu dokumentieren, also Big Endian. Das hat aber die fatale Folge, dass immer Bit 7..0 neben Bit 15..8 steht, also 0 an 15 grenzt und nicht 7 an 8.

Bis die Firma Motorola kam und eine Lösung für den ganzen Spuk hatte - Big Endian. Die Fachleute waren begeistert, insbesondere die Hardware-Entwickler, die immer die einzelnen Strippen verdrahten müssen. Deshalb hat sich auch das Motorola-Konzept in der gesamten Prozess- und Steuerungstechnik rasch durchgesetzt. Man arbeitet einfach vom Großen zum Kleinen, so wie auf dem Papier. Höherwertige Daten kommen zeitlich zuerst. Genial! Damit war das Chaos perfekt.

Das wäre ein typisches Hardware-Interface, wie es sein sollte:

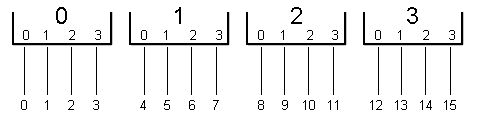
Und so sieht die Praxis aus, zum Beispiel:

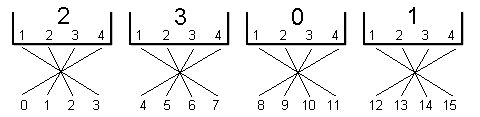
Die Software wird's schon richten.

Das ist zwar nicht genau unser Little/Big- Endian-Problem, ist aber mit diesem verwandt. Bei Wortbreiten von 32 oder 64 bit gibt's entsprechend mehr Vertauschungsmöglichkeiten.

Ein Kollege, der die Aufgabe hatte, auf einem externen Speicher eine CRC-Summe zu prüfen, ist daran schier verzweifelt, weil diese zuerst little endian abgelegt wurde, sich dann aber die Prozessorgeneration geändert hat, die alten Baugruppen aber weiter im Umlauf waren und irgendwann mal mit einer neuen Zentraleinheit Kontakt gehabt haben konnten. Die Lösung war dann die: Man prüfe einmal - wenn falsch, dann die Bytes vertauschen und nochmal prüfen.

Um die Wupptizität weiter zu erhöhen, gibt es heute Prozessoren (z.B. MPC860), bei denen das höchstwertigste Bit (MSB) "Bit 0" und das niederwertigste (LSB) "Bit 31" heißt. Da fällt mir nichts mehr ein.

Wer ist nun schuld an all dem Übel?

Die Römer!

Ich wage zu behaupten: Wenn die damals nicht mit Big Endian angefangen hätten, dann wäre der Dreher vielleicht bei der Übernahme der arabischen Zahlen in unsere von links nach rechts schreibende Welt geglückt. Immerhin hat man's ja versucht, ist aber genau so gescheitert wie heute Intel. In einer durchgängigen Little-Endian-Welt wäre manches einfacher. Aber die Römer haben's versaut.

(Anmerkung: Weder die Römer noch Intel oder Motorola haben Big- oder Little- Endian erfunden. Sie sind hier nur als wichtige Player im o.g. Konflikt genannt.)

Noch ein Beispiel:

Für die nebenstehende Messreihe soll ein Diagramm gezeichnet werden, z.B. ein Geschwindigkeitsprofil, ungefähr so:

Zeit t[s] Geschw. v [m/s] 1 2 10 9 100 80 1000 115

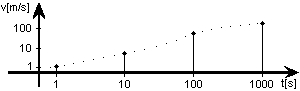
Nun stelle man sich vor, jemand würde Folgendes abliefern:

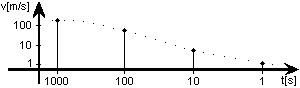
Jeder würde denken: "Der tickt ja wohl nicht richtig - fängt von hinten an."
Aber genau so schreiben wir unsere Zahlen, z.B. die Dezimalzahl 2403.

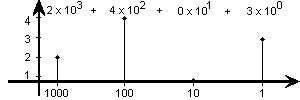
Stellt sich zum Schluss noch die Frage, was mit den anderen Zahlen ist, z.B. Gleitkomma. Der Vorteil von Little Endian liegt doch darin, dass man immer genau sagen kann, wo die Einerstelle ist, nämlich am Anfang. Bei Gleitkommazahlen gibt es aber nur eine Ziffernfolge, die die Genauigkeit repräsentiert, abhängig von der Registergröße; und als zusätzliche Information die Größenordnung (Komma oder Exponent). Bei Gleitkommazahlen ist Little oder Big Endian gleichwertig. (Obwohl, man hätte natürlich auf die Erfindung des Kommas ganz verzichten können und statt dessen nur die ohnehin notwendige Einheit mit der richtigen Größenordnung versehen. Das machen wir ja heute zusätzlich, allerdings nur in Dreierschritten, z.B. Kilo oder Milli. Ich schlage vor: A = 10¹ .. Z = 10²⁶ und a = 10^-1 .. z = 10^{- 26}, kombiniert mit Little Endian und die Einheit vor der Zahl, wie bei der Währung, das wär's doch!) Auch Zahlen in Komplementdarstellung (signed) dürften gleichwertig sein. Das Vorzeichen würde sich immer an der höchstwertigsten Digit-Position am "Ende" der Zahl befinden, egal ob links oder rechts. Vorausgesetzt, auch alle Bits sind konsequent gedreht. Das ist leider bei Little-Endian-Maschinen nicht der Fall.

------

------